Tutorial - Win32 and OpenGL 4.3 - Part3
1. Introduction
This article is mainly intended to give some introductory background information to the graphics pipeline in a triangle based rendering scheme and how it maps to the different system components. We'll only cover the parts of the pipeline that are relevant to understand the rendering of a single triangle with OpenGL (which will be covered in a later post).
2. Graphics Pipeline
The basic functionality of the graphics pipeline is to transform your 3D scene, given a certain camera position and camera orientation, into a 2D image that represents the 3D scene from this camera's viewpoint. We'll start by giving an overview of this graphics pipeline for a triangle based rendering scheme in the following paragraph. Subsequent paragraphs will then elaborate on the identified components.
2.1. High-level Graphics pipeline overview
The basic functionality of the graphics pipeline is to transform your 3D scene, given a certain camera position and camera orientation, into a 2D image that represents the 3D scene from this camera's viewpoint. We'll start by giving an overview of this graphics pipeline for a triangle based rendering scheme in the following paragraph. Subsequent paragraphs will then elaborate on the identified components.
2.1. High-level Graphics pipeline overview
We'll discuss the graphics pipeline from what can be seen in figure 1. This figure shows the application running on the CPU as the starting point for the graphics pipeline. The application will be responsible for the creation of the vertices and it will be using a 3D API to instruct the CPU/GPU to draw these vertices to the screen.
We'll typically want to transfer our vertices to the memory of the GPU. As soon as the vertices have arrived on the GPU, they can be used as input to the shader stages of the GPU. The first shader stage is the vertex shader, followed by the fragment shader. The input of the fragment shader will be provided by the rasterizer and the output of the fragment shader will be captured in a color buffer which resides in the backbuffer of our double-buffered framebuffer. The contents of the frontbuffer from the double-buffered framebuffer is displayed on the screen. In order to create animation, the front- and backbuffer will need to swap roles as soon as a new image has been rendered to the backbuffer.
 |
| Figure 1: Functional Graphics Pipeline |
Typically, our application is the place where we want to define the geometry that we want to render to the screen. This geometry can be defined by points, lines, triangles, quads, triangle strips... These are so called geometric primitives, since they can be used to generate the desired geometry. A square for example can be composed out of 2 triangles and a triangle can be composed from 3 points. Lets assume we want to render a triangle, then you can define 3 points in your application, which is exactly what we'll do here. These points will then reside in system memory. The GPU will need access to these points, this is where the 3D API, such as Direct3D or OpenGL will come into play. Your application will use the 3D API to transfer the defined vertices from system memory into the GPU memory. Also note that the order of the points can not be random. This will be discussed when we consider primitive assembly.
2.2. Vertices
In graphics programming, we tend add some more meaning to a vertex then its mathematical definition. In mathematics you could say that a vertex defines the location of a point in space. In graphics programming however, we generally add some additional information. Suppose we already know that we would like to render a green point, then this color information can be added. So we'll have a vertex that contains location, as well as color information. Figure 2 clarifies this aspect, where you can see a more classical "mathematical" point definition on the left and a "graphics programming" definition on the right.
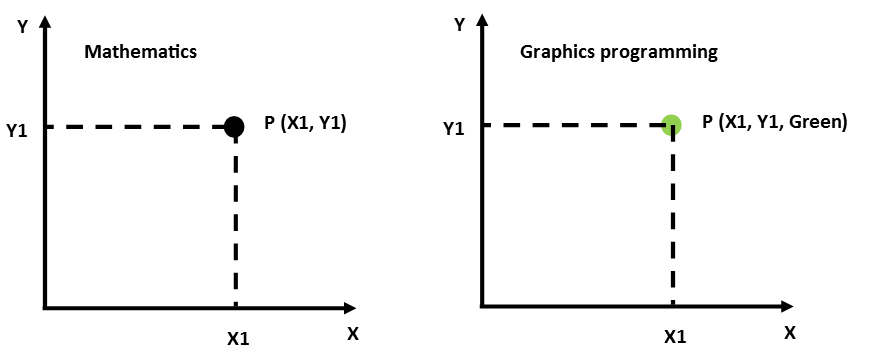 |
| Figure 2: Pure "mathematics" view on the left versus a "graphics programming" view on the right |
Shaders can be seen as programs, taking inputs to transform them into outputs. It is interesting to understand that a given shader is executed multiple times in parallel for independent input values: since the input values are independent and need to be processed in exact the same way, we can see how the processing can be done in parallel.
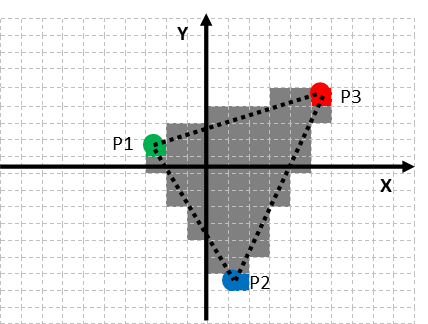
We can consider the vertices of a triangle as independent inputs to the vertex shaders. Figure 3 tries to clarify this with a "pass-through" vertex shader. A "pass-through" vertex shader will take the shader inputs and will pass these to its output without modifying these: the vertices P1, P2 and P3 from the triangle are fetched from memory, each individual vertex is fed to vertex shader instances which run in parallel. The outputs from the vertex shaders are fed into the primitive assembly stage.
 |
| Figure 3: Clarification of shaders |
The primitive assembly stage will break our geometry down into the most elementary primitives such as points, lines and triangles. For triangles it will also determine whether it is visible or not, based on the "winding" of the triangle. In OpenGL, an anti-clockwise wounded triangle is considered as front-facing by default and will thus be visible. Clockwise wounded triangles are considered back-facing and will thus be culled (or removed from rendering).
2.5. Rasterization
After the visible primitives have been determined by the primitive assembly stage, it is up to the rasterization stage to determine which pixels of the viewport will need to be lit: the primitive is broken down into its composing fragments. This can be seen in figure 4: the cells represent the individual pixels, the pixels marked in grey are the pixels that are covered by the primitive, they indicate the fragments of the triangle.
 | |
| Figure 4: Rasterization of a primitive into 58 fragments |
2.6. Fragment shaders
Each of these 58 fragments generated by the rasterization stage will be processed by fragment shaders. The general role of the fragment shader is to calculate the shading function, which is a function that indicates how light will interact with the fragment, resulting in a desired color for the given fragment. A big advantage of these fragments is that they can be treated independently from each other, meaning that the shader programs can run in parallel. After the color has been determined, this color is passed on to the framebuffer.
2.7. Framebuffer
From figure 1, we already learned that we are using a double-buffered framebuffer, which means that we have 2 buffers, a frontbuffer and a backbuffer. Each of these buffers contains a color buffer. Now the big difference between the frontbuffer and the backbuffer is that the frontbuffer's contents are actually being shown on the screen, whereas the backbuffer's contents are basically (I'm neglecting the blend stage at this point) being written by the fragment shaders. As soon as all our geometry has been rendered into the backbuffer, the front- and backbuffer can be swapped. This means that the frontbuffer becomes the backbuffer and the backbuffer becomes the frontbuffer.
Figure 1 and figure 5 represent this buffer swaps with the red arrows. In figure 1, you can see how color buffer 1 is used as color buffer for the backbuffer, whereas color buffer 2 is used for the frontbuffer. The situation is reversed in figure 5.
 |
| Figure 5: Functional Graphics Pipeline with swapped front- and backbuffer |
3. Further reading
If you are interested to explore the graphics pipeline in more detail
and read up on, e.g.: other shader stages, the blending stage... then,
by all means, feel free to have a look at this.
If you want to have an impression of the OpenGL pipeline map, click on the link.
Comments
Post a Comment